2分法,はさみうち法,ニュートン・ラプソン法
2分法
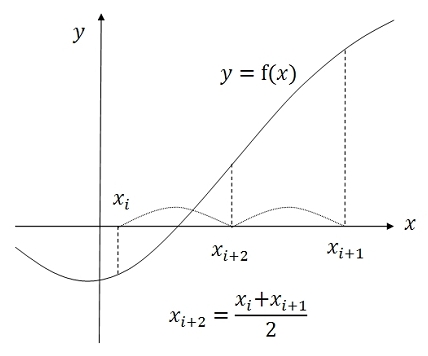
2分法のC++言語サンプルプログラム
// x(i+2)=( x(i)+x(i+1) )/2, |x(i)-x(i1)|<eps
#include <iostream>
#include <iomanip>
#include <fstream>
#include <stdlib.h>
#include <math.h>
using namespace std;
double f( double x ){
return x*x+x-2; //f(x)=(x+2)(x-1)
}
int main(){
double xi=-5.5,xi1=-0.5; //初期値xi,xi1 (xi<xi1)
double xi2,e=0.000001,nmax=5000; //中点,収束判定値,反復最大回数
if( f(xi)*f(xi1)>0 ){ //初期値の適正確認
cout << "f(xi)<0<f(xi1) or f(xi)>0>f(xi1) となるxi,xi1(xi<xi1)を入力してください." << endl;
return 0;
}
for(int i=1; i<nmax; i++ ){ //2分法
xi2=(xi+xi1)*0.5;
if(f(xi)*f(xi2)>0){
xi=xi2;
}
else{
xi1=xi2;
}
if( fabs(xi-xi1)<e ){break;} //収束判定
}
cout << "xi = " << xi << " , f(xi) = " << f(xi) <<endl;
cout << "xi1= " << xi1 << " , f(xi1)= " << f(xi1) <<endl;
cout << "xi2= " << xi2 << " , f(xi2)= " << f(xi2) <<endl;
return 0;
}
コンソール出力結果
xi = -2 , f(xi) = 1.07288e-006
xi1= -2 , f(xi1)= -7.15256e-007
xi2= -2 , f(xi2)= 1.07288e-006
はさみうち法
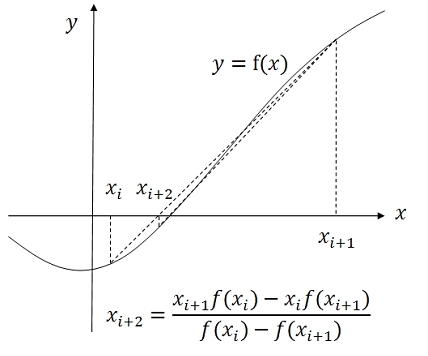
はさみうち法のC++言語サンプルプログラム
// xi2=(xi1*f(xi)-xi*f(xi1))/(f(xi)-f(xi1)), |f(xi2)|<eps
#include <iostream>
#include <iomanip>
#include <fstream>
#include <stdlib.h>
#include <math.h>
using namespace std;
double f( double x ){
return x*x+x-2; //f(x)=(x+2)(x-1)
}
int main(){
double xi=-0.5,xi1=2.0; //初期値xi,xi1 (xi<xi1)
double xi2,e=0.000001,nmax=5000; //2点直線とx軸交点,収束判定値,反復最大回数
if( f(xi)*f(xi1)>0 ){ //初期値の適正確認
cout << "f(xi)<0<f(xi1) or f(xi)>0>f(xi1) となるxi,xi1(xi<xi1)を入力してください." << endl;
return 0;
}
for(int i=1; i<nmax; i++ ){ //はさみうち法
xi2=(xi1*f(xi)-xi*f(xi1))/(f(xi)-f(xi1));
xi=xi2;
if( fabs(xi2)<e ){break;} //収束判定
}
cout << "xi = " << xi << " , f(xi) = " << f(xi) <<endl;
cout << "xi1= " << xi1 << " , f(xi1)= " << f(xi1) <<endl;
cout << "xi2= " << xi2 << " , f(xi2)= " << f(xi2) <<endl;
return 0;
}
コンソール出力結果
xi = 1 , f(xi) = 0
xi1= 2 , f(xi1)= 4
xi2= 1 , f(xi2)= 0
ニュートン・ラプソン法
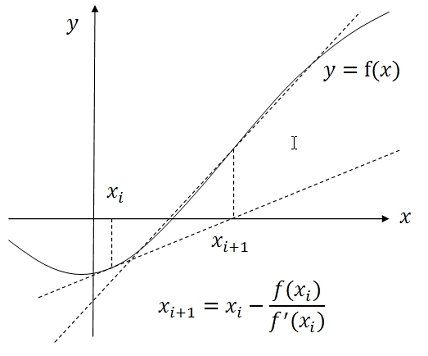
ニュートン・ラプソン法のC++言語サンプルプログラム
// xi1=xi-f(xi)/df(xi), |xi1-xi|<eps
#include <iostream>
#include <iomanip>
#include <fstream>
#include <stdlib.h>
#include <math.h>
using namespace std;
double f( double x ){
return x*x+x-2; //関数f(x)=(x+2)(x-1)
}
double df( double x ){
return 2*x+1; //導関数df(x)=2x+1
}
int main(){
double xi=3.5; //初期値xi
double xi1,e=0.000001,nmax=5000; //接線とx軸交点,収束判定値,反復最大回数
for(int i=1; i<nmax; i++ ){ //ニュートン・ラプソン法
xi1=xi-f(xi)/df(xi);
if( fabs(xi1-xi)<e ){break;} //収束判定
xi=xi1;
}
cout << "xi = " << xi << " , f(xi) = " << f(xi) <<endl;
cout << "xi1= " << xi1 << " , f(xi1)= " << f(xi1) <<endl;
return 0;
}
コンソール出力結果
xi = 1 , f(xi) = 9.92468e-011
xi1= 1 , f(xi1)= -4.44089e-016

